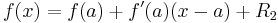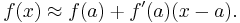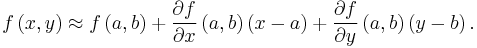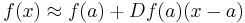Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function (more precisely, an affine function). They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.
Definition
Given a twice continuously differentiable function f of one real variable, Taylor's theorem for the case n = 1 states that
where 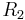 is the remainder term. The linear approximation is obtained by dropping the remainder:
is the remainder term. The linear approximation is obtained by dropping the remainder:
This is a good approximation for x when it is close enough to a since a curve, when closely observed, will begin to resemble a straight line. Therefore, the expression on the right-hand side is just the equation for the tangent line to the graph of f at (a,f(a)). For this reason, this process is also called the tangent line approximation.
Linear approximations for vector functions of a vector variable are obtained in the same way, with the derivative at a point replaced by the Jacobian matrix. For example, given a differentiable function 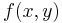 with real values, one can approximate
with real values, one can approximate 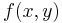 for
for 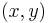 close to
close to 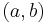 by the formula
by the formula
The right-hand side is the equation of the plane tangent to the graph of 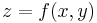 at
at 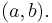
In the more general case of Banach spaces, one has
where 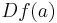 is the Fréchet derivative of
is the Fréchet derivative of  at
at  .
.
See also
- Euler's method
- Finite differences
- Finite difference methods
- Newton's method
- Power series
- Taylor series
References
- Weinstein, Alan; Marsden, Jerrold E. (1984). Calculus III. Berlin: Springer-Verlag. p. 775. ISBN 0-387-90985-0.
- Strang, Gilbert (1991). Calculus. Wellesley College. p. 94. ISBN 0-9614088-2-0.
- Bock, David; Hockett, Shirley O. (2005). How to Prepare for the AP Calculus. Hauppauge, NY: Barrons Educational Series. p. 118. ISBN 0-7641-2382-3.